고정 헤더 영역
상세 컨텐츠
본문

작성자: 17기 김연규
해당 포스팅은 포스텍 전치혁 교수님의 강의 내용을 바탕으로 작성되었습니다.
http://www.kmooc.kr/courses/course-v1:POSTECHk+IMEN677+2021_T2/video
시계열분석 기법과 응용
시계열 데이터 분석을 통하여 시간에 따른 상관관계 등의 패턴 추출 및 이를 바탕으로 미래에 대한 예측을 위한 다양한 기법 학습 및 응용 능력을 배양한다.
www.kmooc.kr
1. VAR(Vector Autoregressive Model)
1) 개요
- 여러 시계열이 병렬적으로 존재할 때, 동시에 고려하여 상호연관성을 분석하는 모형이다.
- 벡터와 행렬을 활용하면 AR 모형과 동일하게 표현할 수 있다.


2) 정상성 확인
- 행렬의 eigenvalue와 determinant를 계산하여 정상성을 확인할 수 있다.

3) 모형 결정
- 모형의 파라미터인 시차 p를 결정하는 것이다.
- ARIMA 모형과 달리 ACF/PACF 그래프를 관찰하여 결정하기 어렵다.
- 현실 상에서는 다양한 정보기준을 산출하여 정보기준 값이 최소인 시차를 선택한다.

4) 모형 분석
- 가장 먼저 할 일은 VAR 모형 자체가 적합한지 확인하는 것이다.
- 그래인저 인과관계 검정을 통해 여러 시계열이 서로 영향을 주는지 확인한다.
- 이후 단위근 검정을 통해 정상/비정상 시계열로 나누어 다른 분석 방법을 적용한다.
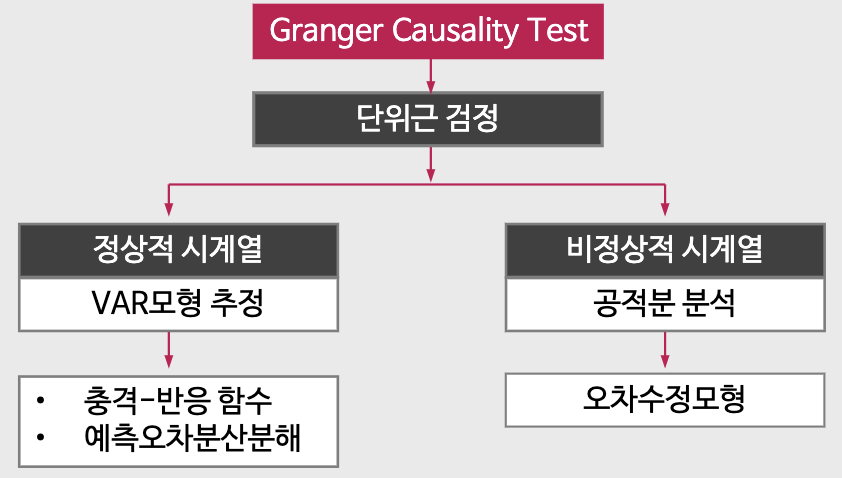
> 그래인저 인과관계
- 정의: 한 시계열 Xt가 다른 시계열 Yt의 미래값을 예측하는 데 도움이 될 때, 그래인저 인과관계가 있다.
- SSE(오차 제곱합)을 산출하여 검정통계량을 계산한다.

4-1) 정상 시계열에서의 분석
(1) 충격-반응 함수(Impulse-Response Function; IRF)
- 한 시계열에 특정 시점에서 충격이 발생할 때, 다른 시계열에 시간에 따라 어떤 영향을 주는지 분석하는 함수.
- 가장 간단한 VAR(1) 모형의 예시를 참고하면 다음과 같다.

→ 시점 1에서 Z1에만 충격이 있었음에도, 시점 2에서는 두 시계열 모두 충격에 반응하여 영향을 받았다.
- IRF를 산출하기 위해서는 분산 행렬 ∑를 분해하여 시계열간 및 오차항간 상관관계를 제거해야 한다.


(2) 예측오차 분산분해
- 현실에서는 특정 시계열의 미래에 여러 시계열의 충격이 영향을 줄 수 있다.
- 따라서 어떤 시계열이 상대적으로 더 중요한지(큰 영향을 미치는지) 파악할 필요가 있다.
- 이를 위해서 미래값을 예측한 후 예측오차의 분산을 시계열별로 분해한다.
- 각 시계열의 분산 비중(기여율)을 비교하여 중요도를 산출한다.
4-2) 비정상 시계열에서의 분석
- VAR 모형은 정상 시계열에 대해 적용한다.
- 따라서 비정상 시계열에 대해서는 차분을 통해 정상화한 후 적용한다.
- 그러나 경제/금융 관련 시계열의 경우 각각은 비정상적이나 장기적으로 균형적 관계를 갖는 경우(공적분 관계)가 있다.
- 이 경우 각각을 정상 시계열로 변환하는 것보다 직접적으로 회귀 모형화하는 것이 더 많은 정보를 얻을 수 있다.
- 유의: 공적분 관계가 없는 비정상 시계열에 대해 회귀분석하면 가성 회귀의 문제(상관관계가 없음에도 유의하다는 결론)가 발생한다.
- 공적분 분석을 위해서는 각 시계열이 동일 차수의 누적 시계열이어야 한다.
(1) 공적분
- 벡터 시계열을 d번 차분하여 정상적일 때, 차수 d의 누적 벡터시계열이라고 하며 I(d)라고 표기한다.
- 차수 d의 누적 벡터시계열이 벡터 a와 선형결합 시 차수 d 미만의 누적 시계열이 될 때, 두 벡터는 공적분 관계에 있다고 한다.
(2) 오차수정모형(Error Correction Model; ECM)
- 여러 시계열이 공적분 관계가 있는 경우, 오차수정모형을 통해 시계열 상호간 단기/장기 효과를 분석할 수 있다.
- 공적분 관계와 ECM 표현은 필요충분조건이다.

(3) 공적분 검정
- Eviews 소프트웨어를 활용하면 Johansen 검정(트레이스 검정과 최대고유치 검정) 결과를 확인할 수 있다.
- 아래 예시를 참고하면 공적분 관계식의 계수가 1에 근접하므로 공적분 관계에 있다는 것과
- 오차수정모형의 계수들의 절댓값을 비교하여 시계열 상호간 효과의 크기를 확인할 수 있다.

2. ARCH / GARCH
ARCH(AutoRegressive Conditional Heteroskedasticity)
1) 개요
- 지금까지의 오차항의 가정과 달리
- 현실의 금융관련 시계열은 잔차의 절댓값 또는 잔차 제곱항이 자기상관관계를 갖는다.
- 더불어 오차항의 분산이 시간에 따라 변한다는 관측 결과가 많다.
- 금융 분야에서 재무상품의 수익률 분산은 변동성이라 하며, 이에 대한 분석이 아주 중요하다.
- 이를 위해서 오차항의 조건부 분산에 대한 ARCH 모형을 활용한다.

2) 표현
- 오차항이 서로 독립이 아니고, 제곱오차항이 AR(q) 모형을 따른다고 가정한다.
- 오차항의 조건부 분산의 형태로 ARCH(q) 모형을 정의한다.

3) 정상성 조건
- 오차항의 조건없는 분산은 상수이지만, 조건부 분산은 확률변수이다.
- 오차항의 조건부 분산과 조건없는 분산의 관계를 통해 정상성 조건을 도출한다.
- 제곱오차항의 계수들의 합이 1보다 작으면 정상이다.

cf. 평균 방정식과 분산 방정식
- 원 시계열 자체의 모형을 평균 방정식이라 하며, ARCH 모형을 분산 방정식이라고 한다.
GARCH(Generalized ARCH)
- ARCH 모형의 일반화 버전이다.
- 기존의 제곱오차항에 조건부 분산항을 추가한 형태이다.

1) 정상성 조건
- ARCH 모형과 동일한 방식으로 유도되며, 계수가 더 추가된 형태이다.

2) 예측
- GARCH 모형을 사용하는 주된 이유는 변동성(조건부 분산)을 예측하기 위함이다.
- ARCH 모형과 마찬가지로 시계열을 예측하는 과정에서 예측오차의 분산을 산출하여 변동성을 예측한다.
- 아래 예시는 가장 간단한 상황(평균방정식: 상수, 분산방정식: GARCH(1,1))을 가정했다.

3) 변형 모형
(1) GARCH-M 모형
- 평균방정식에 조건부 분산을 포함시킨 모형이다.
- 정보의 종류에 따라 영향을 받지 않는 대칭 모형이다.

(2) E-GARCH 모형
- 로그 변동성을 모형화했다.
- 방정식에 오차항의 절댓값과 오차항 자체를 동시에 포함시킴으로써
- 나쁜 뉴스가 좋은 뉴스보다 변동성에 더 큰 충격을 주게 하는 비대칭 모형이다.

(3) T-GARCH 모형
- E-GARCH 모형과 마찬가지로 index function을 추가하여
- 나쁜 뉴스(오차항이 음인 경우)가 미치는 영향이 더 크게 고안한 비대칭 모형이다.

4) 추정
- 최대우도추정법을 사용하며, 로그우도함수를 사용한다.
- ARCH/GARCH 모형의 시차 q는 정보기준으로 결정한다.
5) 검정(LM 검정)
- 잔차 진단에 사용한다.
- 잔차제곱을 사용하여 ARCH 모형(회귀모형의 형태)의 결정계수와 검정통계량을 산출한다.
- 잔차 분석결과 만약 잔차에 ARCH 효과가 남아있다면 잔차에 대한 ARCH 모형을 추가하여 다시 분석해야 한다.
- ARCH/GARCH 모형의 추정 방식은 동일하지만, 추정 결과(유의 여부)는 달라질 수 있다.
'심화 스터디 > 시계열 분석 스터디 (feat.금융)' 카테고리의 다른 글
| 시계열스터디 4주차 엄기영 (0) | 2023.03.30 |
|---|---|
| 시계열 분석 스터디 4주차(우명진): VAR (0) | 2023.03.30 |
| 시계열 스터디 4주차(김태영) : VAR / ARCH / GARCH (0) | 2023.03.30 |
| 시계열 분석 스터디 3주차(김희준) ARIMA, SARIMA (0) | 2023.03.23 |
| 시계열 분석 스터디 3주차(우명진) - ARIMA (0) | 2023.03.23 |





댓글 영역