고정 헤더 영역
상세 컨텐츠
본문

작성자: 17기 김희준
이 글은 포스텍 전치혁 교수님의 강의와 DMQA 김성범 교수님의 강의 내용을 바탕으로 작성되었습니다.
http://www.kmooc.kr/courses/course-v1:POSTECHk+IMEN677+2021_T2/about
시계열분석 기법과 응용
시계열 데이터 분석을 통하여 시간에 따른 상관관계 등의 패턴 추출 및 이를 바탕으로 미래에 대한 예측을 위한 다양한 기법 학습 및 응용 능력을 배양한다.
www.kmooc.kr
https://www.youtube.com/playlist?list=PLpIPLT0Pf7IqSuMx237SHRdLd5ZA4AQwd
# 예측모델
www.youtube.com
1. Box-jenkins ARIMA Procedure
개요
1. Data Preprocessing: 데이터가 정상성이 없는 경우 transformation이나 differencing을 해줘야 함.
2. Identify Model to be Tentatively Entertained
3. Estimate Parameters
4. 진단: 모델이 괜찮다면 예측 모델로 선정, 괜찮지 않다면 2번으로 돌아가기
1. Data Preprocessing
정상성을 검정하기 위해 ACF를 그려봐야 한다.

위의 그래프는 지수적으로 감소하고 있으므로 정상 프로세스, 밑의 그래프는 서서히 감소하고 있으므로 비정상 프로세스이다. 보통 lag2 이후에 확 떨어지면 정상 프로세스이다.
비정상 프로세스이면 어떻게 할까? -> 차분(Differencing)!
2. Identify Model

Graphical Method: ACF, PACF 그래프를 그려놓고 개형을 보고 모델을 택하는 방식. 여기서 절단(cut off)이란, 값이 확 떨어짐을 의미한다.

3. Parameter Method
모델의 파라미터를 설정하여 AIC를 metric으로 평가해본다. 만약 Graphical method에서 차분을 1번 한 MA(1) 모델이 적합하다고 판단되면 ARIMA(0,1,1)으로 AIC 점수를 확인해본다. AIC는 작을수록 좋다.
하지만 2에서 정한 모델이 아닌 다른 모델, 다른 파라미터로도 AIC를 측정해보고 가장 우수한 모델을 최종 선정해야 한다.
파라미터 p,d,q의 여러 경우의 수를 그리드서치해볼 수 있다.
4. Diagnosis – Performance Evaluation
모델이 생성한 예측값과 원본값의 residual로 ACF를 그린다. 이 때 대부분의 값이 임계값 안으로 들어오면 모델을 괜찮다고 볼 수 있다.
Auto covariance, Auto correlation의 수식 도출 과정
X, y가 서로 independent일 때, cov(x, y)=0이므로 다음과 같은 성질들이 성립한다
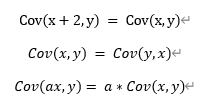
시계열에서 살펴볼 것은 그냥 covariance가 아닌 Auto covariance이다.

Auto covariance의 성질은 다음과 같다.

Auto covariance를 알았으면, Auto correlation도 정의할 수 있다.

위 식은 h 시차가 날 경우의 두 시점 간의 상관관계를 나타낸다.
Auto Correlation의 성질은 다음과 같다.

또한 백색잡음의 auto covariance, auto correlation을 살펴보면 아래와 같다.

ARIMA 모델은 시간에 따라 확률 분포가 일정해야 한다(Constant Probability Distribution). 즉, Stationary Time Series여야 한다. 만약 X_t가 정상성을 지닌다면 아래 식을 만족한다. 즉 시간 t와 관계 없이 Constant라는 것이다.

정상성을 판별하는 간단한 예제를 보자.

위 식을 보면 β_1t가 t라는 시점에 의존하고 있으므로 비정상성을 갖는다.

차분을 한 경우엔 기댓값과 분산이 모두 t 시점에 의존하지 않고 Constant가 나오므로 정상성을 갖는다.
MA와 AR의 수식 도출 과정
MA(1) 모델부터 확인해보자.

위 수식을 활용하여 전개하면 MA(1)의 Auto covariance(γxh) 와 Auto correlation(Ρxh) 은 다음과 같다.

Auto correlation이 앞서 여러 번 그려본 ACF 그래프를 의미한다. Graphical Method에서 살펴본 것처럼, h=2부터 0으로 cut off된다는 것을 볼 수 있다.
이번엔 AR을 살펴보자. AR(1)의 Auto covariance( 와 Auto correlation( 은 다음과 같다.

즉, AR(1)애서의 ACF는 cut off되지 않고 서서히 감소한다.
AR(2)의 Auto covariance(γxh) 와 Auto correlation(Ρxh) 은 다음과 같다.

이 때 AR(2)의 을 Yule-Walker equation이라고 부른다. Yule-Walker equation을 알면 AR(2)의 수식이 주어졌을 때, Auto Correlation을 손쉽게 구할 수 있다.
Backward Shift Operator
ARMA 모델을 소개하기 앞서, Backward shift operator(후방 이동 연산자)에 대한 이해가 필요하다.
Backward shift operator(후방 이동 연산자)는 시계열 시차를 다룰 때 유용한 표기법이다. 아래 수식에서 B 는 데이터를 한 시점 이전으로 옮긴다는 의미이다.

따라서 1차 차분은 아래처럼 수식화할 수 있다.

마찬가지로 2차 차분은 아래처럼 수식화할 수 있다.
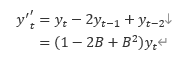
d차 차분을 일반화하면 아래처럼 수식화할 수 있다.

따라서 AR(1)을 Backward shift operator로 표현하면

1항이 at 이고 공비가 ∅B 인 등비급수의 합으로 이해할 수 있다.
마찬가지로 AR(2)도 Backward shift operator을 활용하면 아래처럼 일반화할 수 있다.

ARMA 수식 도출하는 과정
ARMA(1,1)은 AR(1)과 MA(1)이 결합된 형태이다.

ARMA(1,1)을 Backward shift operator로 표현하면

위 식을 통해 ARMA(1,1)의 Auto covariance( 와 Auto correlation( 을 유도하면 다음과 같다.

이제 파라미터 p,q를 상수로 두지 않고 변수로 둔 채 세 가지의 모델의 process를 각각 살펴보면 아래와 같다.

위 식들은 white noise를 input으로 넣었을 때 각각 , 이라는 필터링을 거쳐주는 process로 풀이할 수 있다.
Forcasting의 검증 과정
이제 배운 모델들을 바탕으로 예측(forecasting)을 해야한다.
x1, x2, …, xt가 주어졌을 때 xt+1을 예측하고 싶은 상황을 생각해보자.

만약 지금 상황이 AR(1) 모델로 t+1 시점을 예측을 하는 경우라면 아래처럼 구할 수 있다.

AR(1) 모델로 t+2 시점을 예측하는 것은 아래와 같다.

이번엔 단순히 t+1 시점을 점추정하는 것이 아니라, 아래처럼 구간추정을 해보자.
AR(1) 모델에서 (1-α)*100% 신뢰구간(confidence interval)에서 추정하는 경우이다. 이 때 white noise는 정규분포를 따른다고 가정한다.

유사하게, t+2 시점의 구간추정을 해보자.

이 때 분산 부분이 점점 커지는 것을 확인할 수 있다. 즉 예측 시점이 더 먼 미래가 될수록, 추정 구간은 더 커진다.
이번엔 AR(2) 모델에서 95% 신뢰구간으로 t+3 시점을 추정하는 경우이다.

ARMA(1,1) 모델에 대해서도 살펴보자.


ARMA(1,1) 모델로 t+1, t+2, t+3시점 각각을 (1-α)*100% 신뢰구간(confidence interval)에서 추정하는 경우이다. 이 때 white noise는 정규분포를 따른다고 가정한다.

SARIMA(Seasnal ARIMA)
일반적인 시계열에서 추세는 차분으로 제거될 수 있으나, 계절성은 여전히 남을 수 있다.
이 경우 계절성 차분(seasonal differencing)이란 것을 해주면 계절성이 제거될 수 있다.
계절성 주기를 s로 두면(월별데이터=12, 분기별데이터=4) 아래처럼 계절성 차분을 할 수 있다.

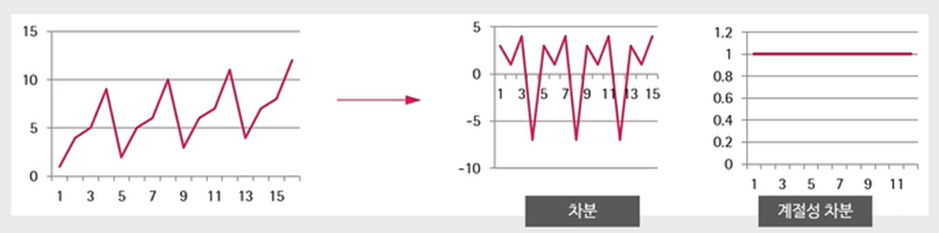
이 원리를 응용한 것이 SARIMA(Seasonal ARIMA) 모델이다.
SARIMA는 데이터를 처리할 때 Non-seasonal한 부분과 seasonal한 부분을 나눠서 처리한다. Non-seasonal한 부분을 처리할 때는 일반 ARIMA 모델과 동일한 (p,d,q) 파라미터를 사용하고, Seasonal한 부분을 처리할 때는 (P,D,Q,m)이라는 새로운 파라미터를 사용한다.
- m: 계절성 시차. 월별 데이터는 12, 분기별 데이터는 4.
- P: 계절적 AR 성분. 일반 ARIMA의 p와 달리, 예를 들어 m=12이고, P=2이면 현재 관측치는 12번째 시차와 24번째 시차의 관측치를 사용하여 추정한다.
- D: 계절적 차분 성분. 일반 ARIMA가 연속된 관측값의 차이를 사용했다면, 여기선 m 시차와의 차이를 이용한다.
- Q: 계절적 MA 성분. 현재 관측치에 대한 과거 잔차의 효과. 예를 들어, m=12이고, Q=2이면 현재 관측값은 12번째 시차와 24번째 시차의 잔차를 사용하여 추정한다.
만약 SARIMA(0,1,1)X(0,1,1,12) 모델이 있다고 하면, 이것은 비계절성 1차 차분 시계열이 MA(1)을 따르며 주기 12의 계절성 1차 차분 시계열이 MA(1)을 따른다는 것을 의미한다.
아래 사항을 고려하여 적절한 차분 실시
- 추세X 계절성O: 해당 주기에 대한 계절성 차분
- 추세O 계절성X: 선형추세가 있는 경우 1차 차분, 곡선 추세가 있는 경우 차분 전에 함수 변환 시도
- 추세O 계절성O: 계절성 차분을 실시하고, 추세 다시 검토 => 여전히 추세가 남아있으면 1차 차분 추가 실시
차분을 하고 나면 비계절성 파라미터 d와 계절성 파라미터 D가 정해진다. 그 후론 p,q,P,Q 파라미터를 찾아야 한다.
이 파라미터들을 결정할 때는 SARIMA 프로세스로 ACF, PACF 그래프를 플로팅해야 한다. 파라미터를 구하는 원리는 ARIMA 때처럼 Graphical Method를 활용한다.
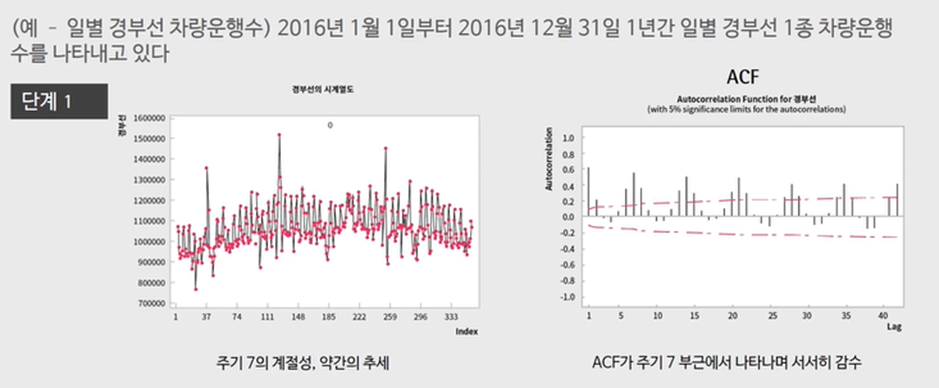
약간의 추세O, 계절성O이므로 일단 계절 차분을 해본다. 계절 차분을 한 결과 추세와 계절성이 모두 제거된다.

계절 차분을 했으니 계절성 파라미터의 D가 1인 반면, 일반 차분은 하지 않았으므로 비계절성 파라미터 d는 0인 점을 유의하자.
하지만 현실적으론 이러한 Graphical Method를 택하기보다도, 여러 경우의 수를 grid search하는 경우가 일반적이다.
'심화 스터디 > 시계열 분석 스터디 (feat.금융)' 카테고리의 다른 글
| 시계열 분석 스터디 4주차(김연규): VAR, ARCH/GARCH (0) | 2023.03.30 |
|---|---|
| 시계열 스터디 4주차(김태영) : VAR / ARCH / GARCH (0) | 2023.03.30 |
| 시계열 분석 스터디 3주차(우명진) - ARIMA (0) | 2023.03.23 |
| 시계열 분석 스터디 2주차(우명진) - 전통 시계열 (0) | 2023.03.23 |
| 시계열 스터디 3주차(신윤): 비정상성 판단, ARIMA, SARIMA, VAR (0) | 2023.03.23 |





댓글 영역