고정 헤더 영역
상세 컨텐츠
본문

ARIMA MODEL
1) ARIMA 모델 정리

Raw Data Plot > stationary인지 아닌지 확인 필요 > Autocorrelation Function 생성 필요
lag가 0일때는 당연히 1 (자기 자신과 계산하기 때)
lag1
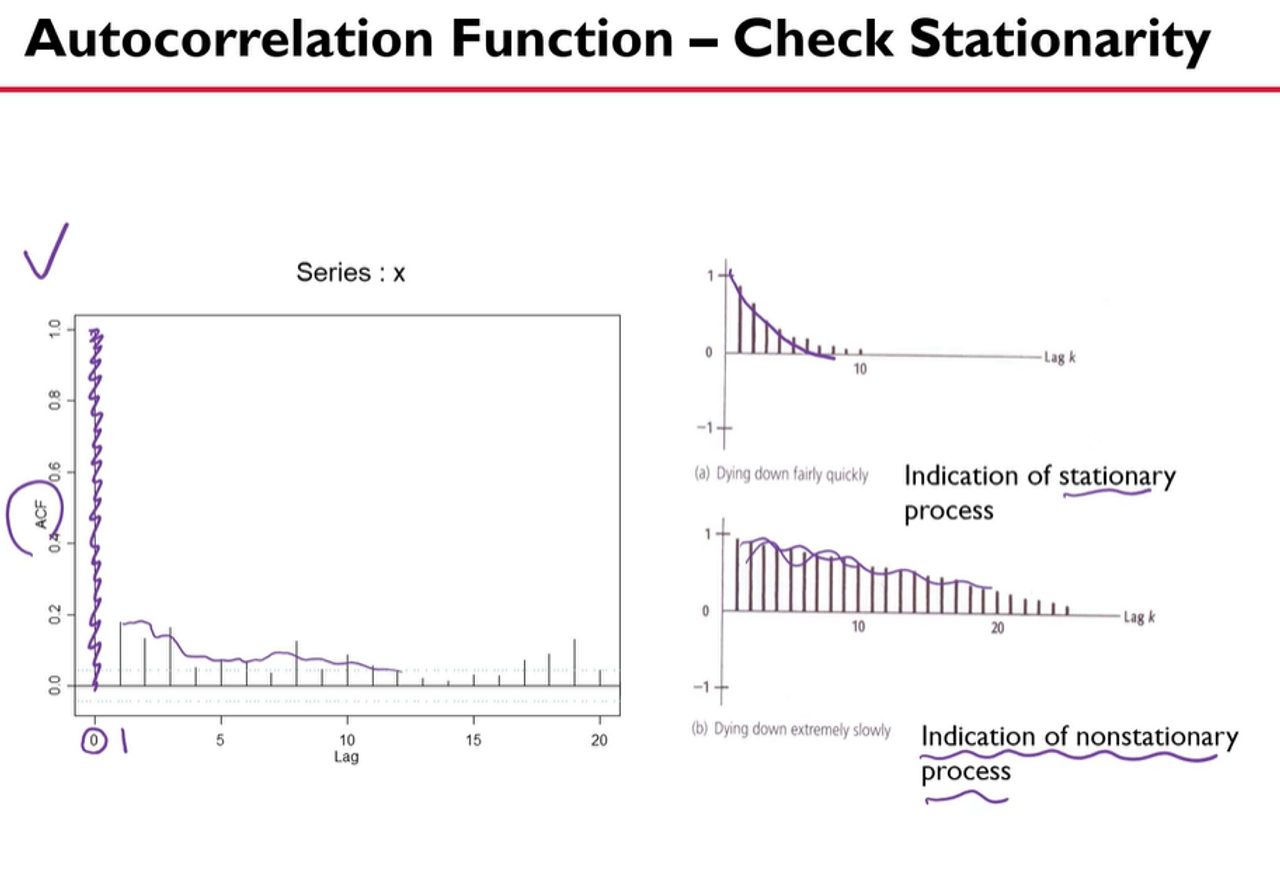
stationary: 빨리 떨어지거나 일정한 패턴 X
Problem: nonstationary → Solution: 차분
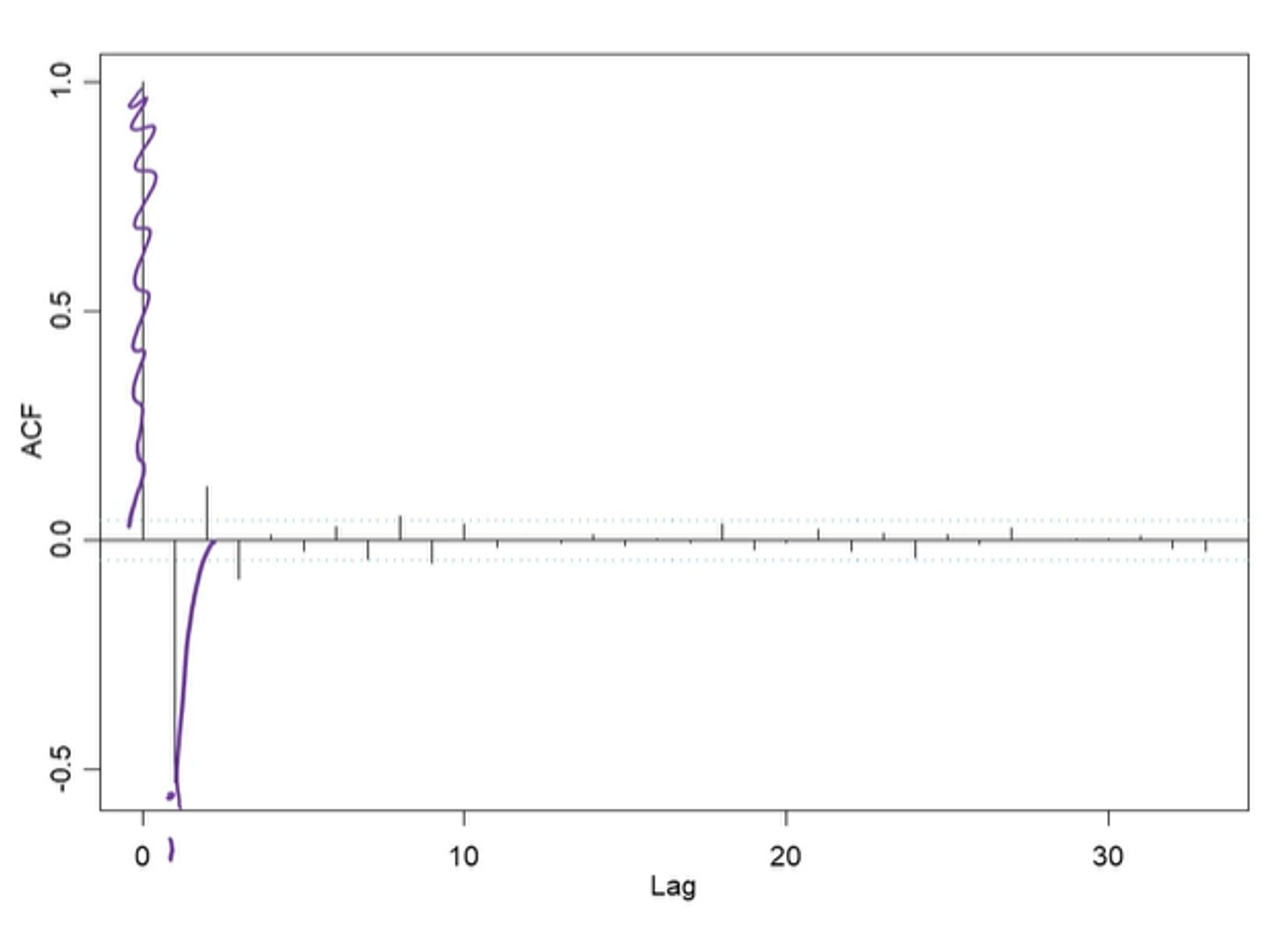
lag 1, 2이후에 확 떨어지거나 일정한 패턴 없는 경우에 stationary



p=0: AR모델
d=1: 차분 한 번 해서 stationary
q=1: lag1이후에 확 떨어졌으니까 MA(q=1) 사용
AIC 적을수록 좋음
2) 비정상적 시계열 모형화를 위한 ARIMA 모형


- ARMA(p,d,q)를 d차 차분하면 ARMA(p,q)가 됨
- 차분 시계열이 ARMA 모형을 따르면 원 시계열이 ARIMA모형을 따른다고 얘기할 수 있음


3) 계절성을 반영한 ARIMA 모델 이해
- 추세는 차분하면 제거 가능 but 계절성은 아님!
- 비계절성은 차분 안 한 게 AR(1), 계절성은 차분한 게 MA(1)

4) 비정상성 검정을 위한 단위근(Unit root) 검정


H0: phi=1 > 단위근이 있는 것 > 시계열 비정상적
phi≠1 > 단위근이 없는 것 > 시계열 정상적

5) VAR 모형의 식별 및 추정 이론

- VAR에서는 오차항이 벡터로 표현됨 + 여러 변수 존재
- 오차항이 다변량 정규분포 따름

- AR(1) → AR(p)로 확장하듯, VAR(1) → VAR(p)로 확장
- 벡터 y와 행렬 F를 마지막 식처럼 정리, VAR(1)형태로 표현 (VAR(p)보다 단순해서 성질 찾기 쉽기 때문)

- 정상성 조건
- AR 모형: 다항식 polynomial의 근이 1보다 크다는 조건 필요했었던 것처럼
- VAR 모형: 계수행렬 phi_1의 eigenvalue가 모두 1보다 작아야 한다는 조건 필요

* VAR 모형의 시차 p 구하기 쉽지 않음 (ACF, PACF 계산하기 쉽지 않음) → 정보기준 information criteria 사용

AIC, SC, HQ 등 작은 것 + 더 작은 시차를 선택
Seasonal ARIMA Model
- 기존 ARIMA 모델에 계절 변동 반영, SARIMA
- ARIMA(p,d,q)(P,D,Q)s
- 월별 계절성(s=12), 분기별 계절성(s=4)

'심화 스터디 > 시계열 분석 스터디 (feat.금융)' 카테고리의 다른 글
| 시계열 분석 스터디 3주차(우명진) - ARIMA (0) | 2023.03.23 |
|---|---|
| 시계열 분석 스터디 2주차(우명진) - 전통 시계열 (0) | 2023.03.23 |
| 시계열 스터디 3주차(조성윤): 비정상성, ARIMA, SARIMA (0) | 2023.03.23 |
| [시계열 스터디 3주차(엄기영)] (0) | 2023.03.22 |
| 시계열 스터디 3주차(김태영) : ARIMA / SARIMA (0) | 2023.03.20 |





댓글 영역