고정 헤더 영역
상세 컨텐츠
본문

지수 평활법 (Exponential Smoothing)
구간평균법
- 과거시점의 일정기간(N)의 평균으로 다음 시점을 예측
- N을 결정N을 결정
- 과거 N기간 동안의 데이터를 평균
- 예측

- 한계
- 과거 n데이터에 동일한 가중치 줌
- 미래의 예측갑이 모두 동일
- 구간(N) 결정하기
- 작은 N: 최근 데이터의 경향 많이 반영
- 큰 N: 과거 데이터의 경향 많이 반영
지수평활법 (Exponential Smoothing)
- 가중 평균 O, 단순 평균 X
- 지수분포 모양에 근거한 가중치 결정
- 최근 데이터에 높은 가중치 / 과거로 갈수록 낮은 가중치

단순지수 평활법 요약
- 현재에 a, 과거에 1-a 가중치
- 보편적으로 a=0.2 혹은 a=0.3 사용
- 대부분의 소프트웨어에서 최적 a값을 자동적으로 계산해줌


이중지수평활법
- 트렌드가 존재하는 시계열 예측 시 적합
- 단순지수평활법 2번 사용

growth: 트렌드라고 보면 됨

ex)

홀트-윈터 (Holt-Winter) 지수 평활법
- 삼중지수평활법
- X 이용 안함 / 자기 자신 (Y)의 과거 갖고 예측
- 계절변동 존재 시 사용되는 방법
- Additive Winter’s Method: 계절 변동 산포 일정할 경우
- Multiplicative Winter’s Method: 계절 변동 산포 증가할 경우

<Additive 홀트-윈터 지수평활법>


<Multiplicativ 홀트-윈터 지수평활법>

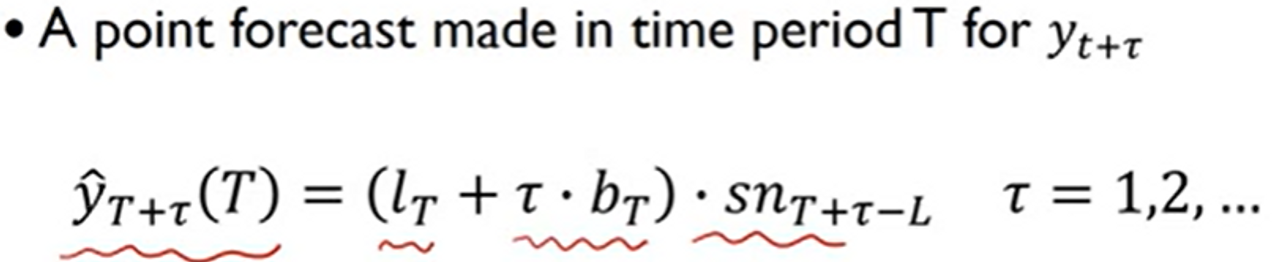
ARIMA 모델 - Part 1
정상 프로세스 (Stationary Process)
- 시간과 관계 없이 평균과 분산 일정
- auto-correlation이 불규칙적으로 나타나는 경우 lag: 현재시점 - n단계 이전 시점 비

비정상 프로세스 (Nonstationary Process)
- 평균 분산 일정 X ACF 감소

AR (Autoregressive) Models
- x 변수: 시점이 다른 y 변수

- multiple regression model과 다른 점
- independence assumption: violated
MA (Moving Average) Models
- t 시점의 데이터를 t 이하의 error들로 표현
- 연속적인 error terms로 y와의 관계 표현

ARMA (Autoregressive and Moving Average)
- AR + MA 모델

ARIMA (Autoregressive Integrated Moving Average)
- AR, MA, ARMA : data → stationary by differencing
- ARMA : fitted differencing = integrated
- ARIMA의 I: differencing을 몇 번 했는지 보여줌
- p : AR 모델의 independent var의 개수 q: MA 모델의 parameter의 개수 d: differencing의 개수

차분 (Differencing)
- 현 시점 데이터에서 d시점 이전 데이터를 뺀 것

- 간단한 trend: 1차 차분으로 충분 복잡한 trend: 2차 차분 필요
캐글 코드 실습
EDA, ACF, AR, MA
https://www.kaggle.com/code/chirag19/time-series-analysis-with-python-beginner
MA 종류
https://towardsdatascience.com/how-to-code-different-types-of-moving-averages-in-python-4f8ed6d2416f
Holt-Winter 포함 예측부터 평가까지
https://www.kaggle.com/code/prakharprasad/smoothing-holt-winters-forecast
'심화 스터디 > 시계열 분석 스터디 (feat.금융)' 카테고리의 다른 글
| 시계열 스터디 3주차(김태영) : ARIMA / SARIMA (0) | 2023.03.20 |
|---|---|
| 시계열 스터디 2주차(김희준) (0) | 2023.03.17 |
| [시계열 스터디 2주차(엄기영)] (0) | 2023.03.16 |
| 시계열 스터디 2주차(조성윤) (0) | 2023.03.16 |
| [시계열 스터디 1주차(김희준)] (0) | 2023.03.15 |





댓글 영역