[논문 리뷰 스터디] Review of Functional Data Analysis (Part 1)
작성자: 16기 민윤기

1. Introduction
- FDA란?: functions, images, shapes(curves) 등의 형태로 이루어진 데이터에 대한 분석 방법론
- 본질적으로, infinite dimensional인 경우가 많음
- 목적은 여타 통계적 분석의 목적과 같이 표본이 뽑힌 모집단에 대한 추론
- 1세대 functional data: 독립적인 실함수로 구성된 random sample -> curve data라고 일컬어짐
- Next generation functional data: brain & neuroimaging data
- 데이터를 변환, 재표현, 그림 제공, 반응변수의 변동의 중요한 요인을 파악
- 예) 시간에 따른 기온의 변화 데이터: 연속적인 성질에도 불구하고 관측의 속성상 이산형으로 나타남
- FDA의 특징
- functional data에 대한 rigorous definition은 아직 완전하지 않음
- 가장 특징적인 것은, 데이터가 개별적인 관측치의 연속체가 아니라 하나의 형태를 가지고 관측된 함수
- dense data와 sparse data로 나뉘는데, sparse data는 각각이 다른 시점에 관찰되는 종단 연구를 의미함
- 측정 방법(sampling plan)에 따라 FDA의 현상(수렴율 등)이 달라짐
- 특정 시점마다 이산형 형태로 관측되는 데이터는 대부분 오차가 존재하여, 다양한 평활화 기법이 요구됨
- Sparse/irregularly sampled functional data

-> 각 개인별로 상이하고 불규칙적으로 측정되면서 생기는 plot의 불규칙함
따라서, 오차 없이 관측된 functional data는 확률적 과정을 근거로 다루기 쉬움(functional law of large numbers, functional central limit theorems 등 적용 가능)
- 일반적인 linear/generalized linear model에서 변형된 functional regression의 관점에서, 고차원의 functional data를 다루기 위한 demension reduction은 핵심 요소임
- clustering과 classification 역시 유용하고 중요한 FDA의 tool 중 하나임
- 가정: 데이터에 내재하는 함수가 smooth 해야함(derivative를 구할 수 있도록)
- 대표적인 data handling 기법: smoothing methods, notably kernel, local least squares, spline smoothing
2. Mean and Covariance Function, Functional Principal Component Analysis
- Estimator of Mean and Covariance


- 관측되는 $Y_ij$에 대한 notation: $Y_ij = X_ij + e_ij$ ($e_ij$는 measurement errors)
- 가정: error의 등분산성 -> $(sigma^2)_ij$ = $sigma^2$ (꼭 필요한 가정은 아니지만 분석의 용이함을 위해 가정함)
- Estimate of mean and covariance:


- Sampling schedule이 각 대상마다 다르면, estimate을 동일한 방법으로 구할 수는 없음 -> 그러나, nomparametric smoother(ex. local polynomial estimate) 등을 산점도에 적용 가능 -> $mu(t)$에 대한 consistent estimates 구할 수 있음
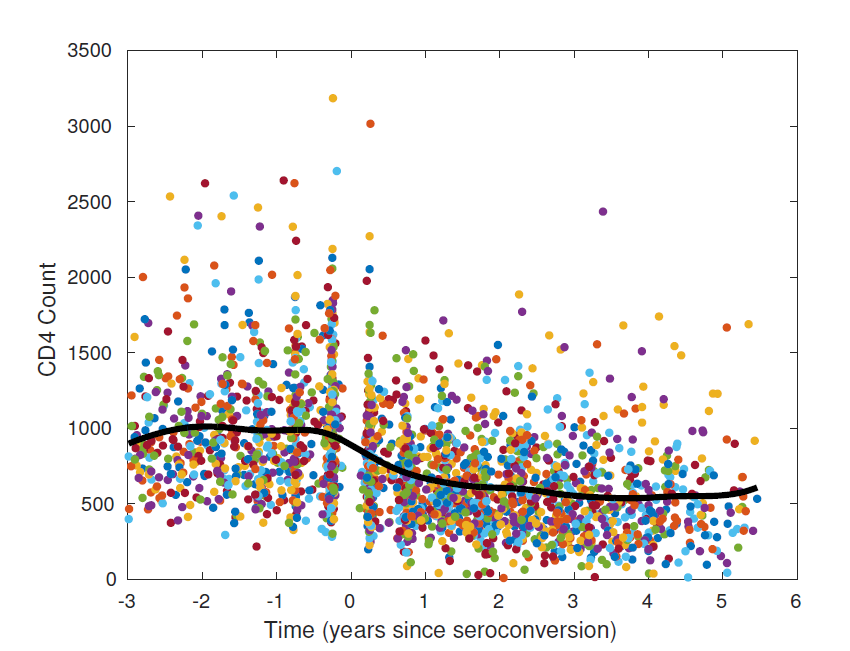
- Hypothesis Testing and Simultaneous Confidence Bands
- Suggestions: two-sample test and ANOVA test 또는 dense functional data에 대한 '동시신뢰구간'
- 문제점: 데이터의 무한 차원 + target function의 비모수적 성질
- dense data에 대해서는 estimated mean process는 Gaussian process로 수렴함 -> 근사된 Gaussian 분포를 이용한 평균에 대한 근사신뢰구간을 구할 수 있음
- 정리하면, functional data의 특성(ultra-dense, dense, sparse)에 따라 동시신뢰구간을 구하는 방식이 차별화 되어야 함 -> dense data는 일반적인 모수적 추론이 가능
- bias는 독립적으로 측정되고, 적절한 asymtotic theory가 존재하고, estimator의 정규성 조건을 충족시키는 것을 기대함
- ultra-dense: $sqrt(n)$은 asymtotic bias 없이 수렴율로 재현됨
- dense: bias가 존재하지만, 수렴율은 $sqrt(n)$으로 근사할 수 있음
- sparse: dense와는 다른 paradigm을 따르게 됨 -> $sqrt(n)$보다 느린 수렴율을 갖게 됨(measurement design에 의존함)
- Functional Principal Component Analysis(FPCA)
- PCA: 다변량 데이터에 대한 핵심 차원 축소 기법 -> extended to FPCA
반응변수들을 선형변환시켜, 주성분이라고 부르는 서로 연관되어 있지 않은, 독립적인 변수를 유도 - FPCA: 무한 차원의 함수적 데이터를 유한 차원의 scores 벡터로 변환(일반적인 PCA 방법론을 차용)
- 데이터 변동성의 형태를 찾기 위해 계산 가능한 유한한 주성분 요소를 찾음으로써 함수적 데이터의 차원 축소
- 첫번째 주성분은 자료 변동의 가장 많은 부분을 설명하며, 두번째 주성분은 첫번째 주성분과 직교하는 변동을 설명하는 식으로, 몇 개의 주성분을 통해 데이터 변동의 거의 전부를 설명할 수 있음
- 관측된 데이터의 함수적 표현: $x_i(t)$ (i = 1, ... , n)이 모든 t에 대해 '$sum x_i(t)$ = 0'을 만족시킨다고 가정
- 함수적 데이터의 공분산 함수:

-> 적분변환을 사용하여 고유값과 고유함수($psi$)로 나타낼 수 있음
-> 주성분 함수를 찾기 위해서는 eigen value에 대한 고유방정식을 만족하는 해 찾기

-> 고유값의 크기에 따라 주성분 함수의 순서 정해짐
- Applications of FPCA

- 첫번째 eigen function은 데이터의 총 변동의 84%를 설명함
- 이외 세번째와 네번째의 eigen function은 중요치 않다고 판단
- 첫 eigen function은 시간에 따라 constant한 특성이 있음 -> random intercept가 총 변동에 크게 영향을 미침
Ex) 우리나라 68개 기상 관측소에서 30여년간 매월 측정한 기온 (=> 주기: 12)
- 따라서, 12개의 푸리에 기저와 상수항을 이용하여 이산형 관측치들을 함수적 데이터로 변환
- Cf) 푸리에 기저: 데이터의 평활화(smoothing)하는 기법 중 하나 -> 기저 함수의 선형 결합으로 데이터 표현 ->
푸리에 기저는 주기적이고 급격한 변화가 없는 함수에 대해 특히 유용하게 적용됨
- Cf) 푸리에 기저: 데이터의 평활화(smoothing)하는 기법 중 하나 -> 기저 함수의 선형 결합으로 데이터 표현 ->


- 대체적으로 사인 함수의 형태를 띠는 것을 확인할 수 있음

- 예상과 같이, 여름철에 높은 기온과 뚜렷한 사계절의 형태 드러남 + 분산의 경우, 여름철이 겨울철보다 작다는 것 -> 겨울철에 지역별로 기온 차이가 더 크게 나타남을 알 수 있음

- 첫번째 주성분이 전체 변동성의 약 80%를 설명하고 있으며, 우리나라 기온의 11월 말 부터 다음 해 1월 말까지, 즉 겨울철 변동성을 잘 설명하고 있음
- 두번째 주성분은 전체 변동성을 약 19% 설명하며, 여름철의 변동성을 설명함
주성분의 우선순위를 고려하여, 우리나라 기온의 변동성은 겨울에 더 크다는 결론을 내릴 수 있음
3. Correlation and Regression: Inverse Problems and Dimension Reduction
- Functional Regression
- 반응변수나 공변량이 functional data를 포함하는 경우의 회귀분석
- 모델은 선형, 비선형, 부분적 선형 모두 가능
- Model with Scalar Response

- $X$를 functional covariate $X^c$ = X(t) - $mu(t)$로 대체
- $beta$는 $beta(t)$로 대체

- $beta$와 $X$를 같은 함수적 기저의 선형결합 형태로 표현(orthonormal basis) -> basis expansion
- 자주 사용되는 방법 중 하나인 B-spline regression
- Spline regression: 기저 함수의 선형결합으로 회귀 모형을 근사하는 비모수 추정법
functional data의 특성 상, 무한개로 이루어진 선형결합을 계산하기 어려우므로 유한개로 근사 - 일반적인 regression처럼 LS method로 $b^hat$ 추정
- Spline regression: 기저 함수의 선형결합으로 회귀 모형을 근사하는 비모수 추정법

- Using orthonormal basis,


- Multiple functional regression, generalized linear model로도 확장 가능